Snadné parametrické studie a optimalizace v programu Ansys DesignXplorer

Snadné parametrické studie a optimalizace v programu Ansys DesignXplorer

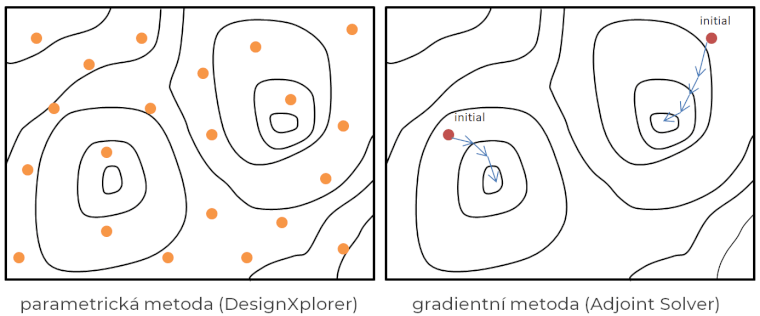
Nástroj DesignXplorer (DX) lze zařadit do kategorie parametrických optimalizací. Podstatou optimalizace je tedy hledání takových vstupních parametrů (podmínek), při kterých nabývají výstupní parametry požadovaných optimálních hodnot (např. min, max). Parametrickou optimalizaci můžeme porovnat (Obr. 1) například s gradientní optimalizací, která spočívá v hledání ideálního tvaru dle definovaného kritéria za pevně daných podmínek. Tento druh optimalizace lze provádět např. v programu Ansys Fluent pomocí Adjoint řešiče. Jiné simulační programy mají často své vlastní nástroje na optimalizaci. Výhodou DesignXploreru je jeho univerzálnost. Lze jej totiž aplikovat na většinu simulací z programů od společnosti Ansys, ale také na externí řešiče jakými jsou např. MS Excel nebo Python. Pokud se tedy naučíte pracovat s DX, budete schopni optimalizovat široké spektrum úloh.

Obr. 1: Grafické srovnání přístupů parametrické a gradientní optimalizace.

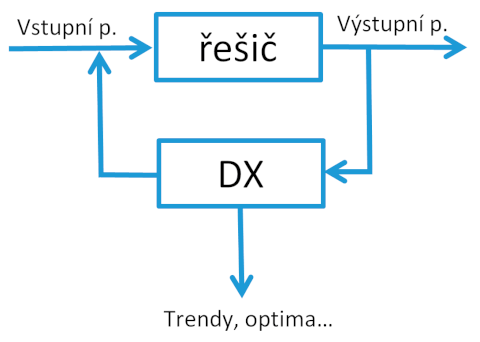
DesignXplorer se spouští v prostředí Workbench, které je pro mnoho uživatelů známé. Pro možnost využití funkcí DX je třeba definovat alespoň jeden vstupní a jeden výstupní parametr v rámci některého z řešičů. Jak již bylo zmíněno, řešičem může být např. některý z mnoha Ansys softwarů, který pro dané hodnoty vstupních parametrů spočítá hodnoty parametrů výstupních. DX přebírá pouze tyto hodnoty, a je tak nezávislý na volbě řešiče. Tento mechanismus je demonstrován na Obr. 2.

Obr. 2: Schéma aplikace DesignXploreru.

Funkce DesignXploreru

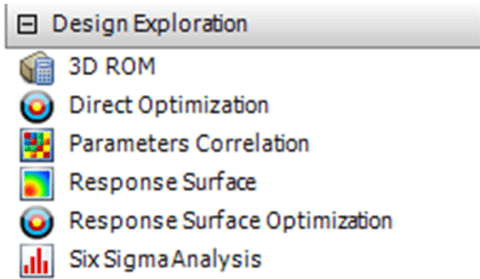
Součástí DesignXploreru je šest funkcí zařazených do stromové struktury pod názvem Design Exploration (Obr. 3). Dvěma hlavními způsoby optimalizace v DX jsou funkce Direct Optimization a Response Surface Optimization. v rámci těchto funkcí je možné si k optimalizaci vybrat z šesti algoritmů (Screening, MOGA, NLPQL, MISQP, Adaptive Single-Objective a Adaptive Multi-Objective).

 Obr. 3: DX funkce ve stromové struktuře Workbench.

Direct Optimization lze aplikovat přímo na připravený problém s definovanými parametry. Při této variantě jsou podle optimalizačního algoritmu měněny vstupní parametry za účelem nalezení požadovaného optima. V závislosti na druhu optimalizačního algoritmu a druhu problému je nutné zopakovat simulaci s rozdílnými hodnotami parametrů řádově stokrát až tisíckrát. Tento postup je vhodný v případě, že vyhodnocení výstupních parametrů na základě změny vstupních parametrů je časově nenáročné, tedy v případě relativně rychlé simulace.

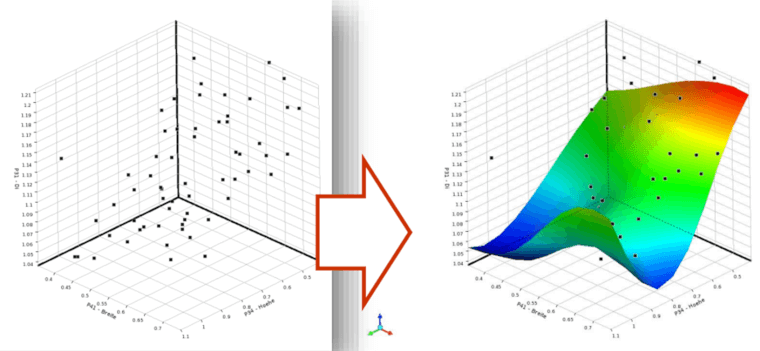
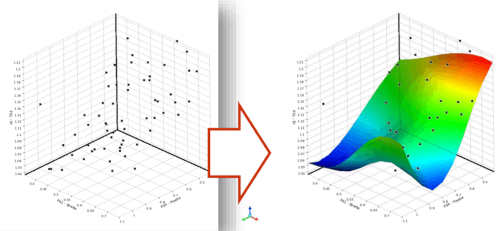
Pokud je ovšem vaším řešičem simulace obsahující velké množství buněk a simulace je časově náročná, není postup přímé optimalizace vhodný. Pro tento případ se hodí funkce Response Surface Optimization, která výrazně snižuje počet simulací potřebných pro optimalizaci, a tudíž celý proces urychluje. V tomto případě je nejprve pomocí „chytrého výběru“ (Design of Experiment) vybrána sada bodů (Design Points), jež je tvořena kombinacemi vstupních parametrů tak, aby tyto body co možná nejreprezentativněji popsaly definovaný problém. Získané hodnoty výstupního parametru jsou poté proloženy plochou (Response Surface), viz Obr. 4. V následné optimalizaci jsou výstupní parametry získávány pouze jako funkční hodnoty vytvořené plochy, což má za následek zmiňovanou úsporu času. Při hledání optim touto metodou je třeba mít na paměti, že správnost výsledků je závislá na správnosti proložení bodů plochou (Response Surface). Za tímto účelem nabízí DX několik ukazatelů správnosti proložení.

Obr. 4: Proložení vypočtených bodů plochou – Response Surface.

Kromě výše popsaných funkcí, které jsou nejčastěji používány k optimalizacím, nabízí DX funkci Parameters Correlation. Tato funkce poskytuje informace o tom, jak moc jsou výstupní parametry ovlivňovány změnou vstupních parametrů. Provádět parametrickou studii je doporučováno v případě většího množství vstupních parametrů za účelem jejich možné redukce, jelikož s přibývajícím počtem vstupních parametrů výrazně roste počet potřebných simulací, a tudíž i výpočetního času.

Funkce Six Sigma Analysis nabízí možnost probabilistického přístupu k optimalizaci. Vstupní parametry nejsou zadány pomocí spodní a horní meze jako je tomu při tradiční optimalizaci, nýbrž jsou definovány pomocí středních hodnot s jejich odchylkami a rozložením. Výstupem této optimalizace může být například pravděpodobnost, se kterou bude dodržena nějaká bezpečná hodnota výstupního parametru.

V neposlední řadě poskytuje DX možnost tvorby redukovaného modelu pomocí funkce 3D ROM. Redukované modely nabízí rychlé řešení jinak časově náročných výpočtů pomocí matematické reprezentace daného problému.

Ideální chlazení součástky

Pro ilustraci byl vytvořen problém chlazení součástky vzduchem proudícím skrz žebra (Obr. 5). Vstupními parametry jsou tloušťka a počet žeber. Výstupním parametrem je průměrná teplota součástky, kterou chceme minimalizovat.

Obr. 5: Model součástky s žebry.

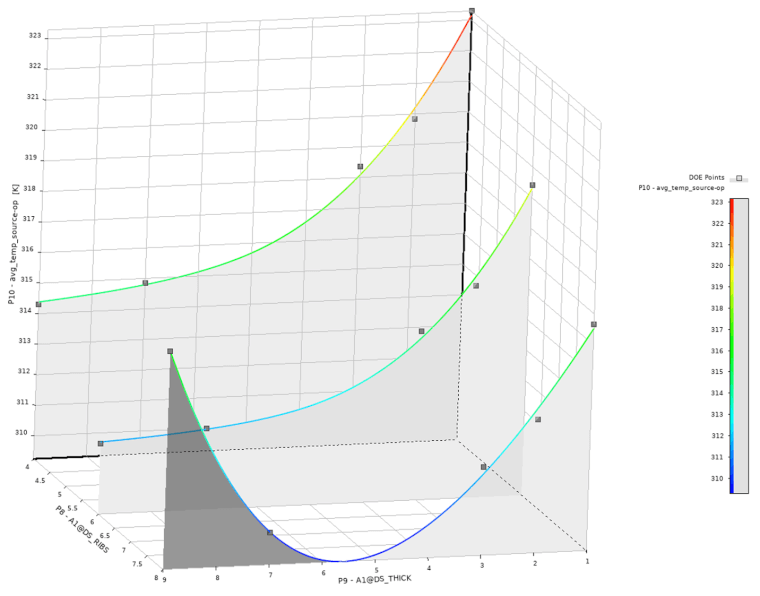
Pomocí nástroje Design of Experiments bylo vytvořeno patnáct pracovních bodů, skrz které byla následně proložena plocha popisující teplotu součástky při změně parametrů žeber (Obr. 6). Z tohoto grafu je patrné, že při počtu osmi žeber a tloušťce žebra přibližně 5,5 mm je dosaženo minimum průměrné teploty. Z optimalizace pomocí Response Surface Optimization bylo minimum nalezeno při stejném počtu žeber a tloušťce 5,6 mm s hodnotou minima 309,3 K. Pro ověření správnosti byla vypočtena simulace s těmito vstupními parametry a odpovídající hodnota teploty činila 310,1 K. Pokud je pro uživatele tato odchylka (0,25 %) přijatelná, můžeme problém uzavřít s tím, že pro nalezení optima za daných podmínek stačilo provést simulaci pouze šestnáctkrát. V případě, že by byla vyžadována větší přesnost, je možné nově nalezený bod (8 žeber; 5,6 mm tloušťka; 310,1 K teplota) přidat jako šestnáctý Design Point a znovu proložit body křivkou. Tímto způsobem se lze iterativně dosáhnout požadované přesnosti.

Obr. 6: Vytvořený Response Surface s viditelným minimem.